Outsource: Gamedev.net

I came across gamedev.net in some of my research, and only recently got around to really browsing the site.  It appears to have quite a few interesting articles, some of which are directly pertinent to what I'm trying to accomplish in my own project.

This article discusses some basic (though powerful) concepts related to multi-player local (single-machine) games.  Hidden within the article is the also-simple (though even more powerful) concept of designing for scalability—avoiding implementing specific limitations where possible.

This page is an interesting FAQ for dealing with network gaming.  I'm not yet sure whether I'll ever move into the online space with this project, but if I ever do, I'm sure I'll find this an invaluable resource.

I'm sure there are tons of other pages on the site that are useful and interesting.  These two caught my eye for now, though.

3D Transformation Matrix Summary and Derivations

Translate

Derivation

Scale

Derivation

Rotate Around z-axis

Counter-Clockwise

Derivation

Clockwise

Derivation

Rotate Around y-axis

Counter-Clockwise

Derivation

Clockwise

Derivation

Rotate Around x-axis

Counter-Clockwise

Derivation

Clockwise

Derivation

Rotate Around Arbitrary Axis 
—Defined by the unit vector (u, v, w)

Counter-Clockwise

Derivation

Clockwise

Derivation

---

Derivation: Translate

Derivation: Scale

Derivation: Rotate Around z-axis (Counter-Clockwise)

Derivation: Rotate Around z-axis (Clockwise)

Derivation: Rotate Around y-axis (Counter-Clockwise)

Derivation: Rotate Around y-axis (Clockwise)

Derivation: Rotate Around x-axis (Counter-Clockwise)

Derivation: Rotate Around x-axis (Clockwise)

Derivation: Rotate Around Arbitrary Axis (Counter-Clockwise)

1. Rotate vector around z-axis (clockwise): R_z
2. Rotate vector around y-axis (clockwise): R_y
3. Rotate around vector (counter-clockwise): R
4. Rotate vector around y-axis (counter-clockwise)*: R_y^-1
5. Rotate vector around z-axis (counter-clockwise)*: R_z^-1

* The inverse of a rotation matrix is the same as the rotation matrix for the same angle in the opposite direction.
Total Rotation Transformation: R_z^-1R_y^-1RR_yR_z
= (R_z^-1R_y^-1)(R)(R_yR_z)
First and Last Rotations (R_z and R_z^-1)


Second and Second-to-Last Rotations (R_y and R_y^-1)


Middle rotation (R)

First two rotations combined (R_yR_z)

Final two rotations combined (R_z^-1R_y^-1)

Final three rotations combined (R_z^-1R_y^-1R)

Entire transformation ((R_z^-1R_y^-1R)(R_yR_z))

Derivation: Rotate Around Arbitrary Axis (Clockwise)

See the previous section, and change the sign of each sin() function.

OpenGL Camera Transformations for a Third-Person View

OpenGL doesn’t have a camera, per se, like you might find in a traditional CAD application.  Instead, it renders to the screen the view from the original origin, looking along the z-axis toward the negative direction (that is, z+ is coming out of the screen toward you).  The x-axis is horizontal, with x+ going to the right side of the screen, and the y-axis is vertical, with y+ going to the top of the screen.  The origin starts out centered in the widget that handles the rendering.

Using OpenGL is somewhat like trying to take a group photo in front of a landmark, where the camera stays in one position and the people are themselves moved around within the scene.  In order to get the appearance of moving the camera, the entire OpenGL scene can be moved.

There are two basic ways of viewing an OpenGL world: perspective and orthographic views.  There are various OpenGL tutorials which discuss the differences between the two, and how to set them up.  It suffices me to mention that I’m using a perspective view, since it provides a more "real" 3D experience.

Three basic transformations can be performed in OpenGL: translate, rotate, and scale.  Each transformation only affects the objects drawn after the transformation is made.  Translate moves the origin to a new position; rotate changes the directions of the axes; scale changes the size of the basic unit.

Each object in the 3D world should be drawn in its own coordinate space—that is, with the origin (0, 0, 0) and the standard axes having meaning in the context of the object, without regards to any other object.  In my game, the player agent's origin is quite different from the maze's origin, and is also quite different from the origin of any other agent.  Each agent may have a different orientation from another, as far as the maze is concerned, but "forward" is always along the agent's own y-axis.  It is possible that agents may experience life on different scales (an ant compared to a giant, for example), but for my purposes, scaling is largely ignored.

Transformations are the way to set the origin and axes properly so that, when the agent (or other object) is drawn, it is done within its own coordinate space.  In the case of a third-person camera, a transformation should occur to place the agent's origin at some point in front of the camera.  We will use a translate to move the origin ten units along the z-axis into the screen (in the negative direction): glTranslated(0, 0, –10).  From this point forward, any operations performed will refer to the new origin.  (The image to the right demonstrates the translate transformation.)

My world will assume that the xy-plane is horizontal, with z+ pointing toward the sky.  If I were to draw the maze, at this point, the camera would be looking down on it from directly overhead.  I would prefer to see the world from an over-the-shoulder kind of view, so I will need to perform a rotate transformation.  My player is facing the y+ direction (along the green line, in the image above), so to move the camera so that it is facing the same general direction, I will have to rotate around the x-axis (the red line).  A positive angle of rotation will point the y-axis more toward the camera, which is opposite the effect we're trying to create.

In the image to the right, the original axis orientation is shown using dashed lines, while solid lines show the orientation after the rotation around the x-axis has been performed.  The cylinder demonstrates the position of the agent, relative to the camera.  This gives us an over-the-head view (if we were going for a true over-the-shoulder view, we would have simply translated the origin along the x-axis before drawing the object).

Here is another perspective on the same scene, showing the agent's cylinder in its own coordinate space.  Note that the axes look more traditional, with the xy-plane lying horizontally.  Note also that we have also performed another translate transformation.  In order to begin drawing the maze in its own coordinate space, the origin must be moved to the proper location.

I consider this to be the world coordinate space.  Everything, from this point forward, can be built in terms of the current position, without worrying about the camera.  Before performing any further transformations, use glPushMatrix() to store the current position, and the corresponding glPopMatrix() will return you to working in world coordinate space.

***

Note that this is not the exact series of transformations and drawing that I'm actually using.  For my program, I'm expecting any number of agents, any one of which could be followed by the camera.  While it's possible to do things exactly as I've done here, and simply draw the currently-followed agent separately from the other agents, it makes much more sense to me to draw all of the agents at the same time.  In that case, the initial transformations are the same, to get the camera into the proper position.  However, the agent is not drawn until after the world coordinate space is determined—along with all the other agents.

Note also that I did not give my cylindrical agent in this example any rotation within the world coordinate space.  That rotation would have occurred immediately before the translation in the last image, after the agent had been drawn (so it would continue to face forward).  If the agent were to look 45 degrees to the right, the scene would instead be rotated 45 degrees to the left (counter-clockwise, around the z-axis).

Agent Rotation: Groundwork

After I figured out the two-dimensional rotation math, I changed my agent's "direction" arrow.  Initially, it was a collection of lines (GL_LINES) which were rotated around the z axis by the required angle, using the OpenGL rotated function.  Instead of using my home-grown rotation math to determine the new vertices for each endpoint of each of the arrow's lines, I decided to keep it simple.

I still need to update the direction vector manually.  However, I can use OpenGL's functions to rotate as many points at a time as I require (that is, the entire agent 3D object).  In order to determine that my vector rotation and the OpenGL rotation were in-sync, I decided to draw a representation of the direction vector in the world coordinate space (translated to the origin of the agent object) as a simple line, and to draw a more complex agent object in its own coordinate space (rotated with OpenGL).  Here are the steps for each frame:

• Initialize the canvas
• Translate to set the camera's position
• Draw the board, using world coordinates
• Push the OpenGL transformation matrix (this allows us to draw each agent individually, without regards to the others)
• For each agent...


• Translate to the agent's position
• Push the transformation matrix again (this allows us to draw the direction vector after the object itself has been drawn)
• Rotate around the z axis, to put OpenGL into the agent's coordinate space
• Draw the agent object
• Pop the previously-pushed transformation matrix, to return to world coordinates (centered at the origin of the current agent)
• Draw the direction vector
• Pop the transformation matrix again, to center once again at the world's origin (permitting the next Translate to move the coordinate system center to the origin of the next agent)

What I initially found was that the direction vector and the object did not stay aligned.  The reason for this is that OpenGL's rotation functions are calculated in degrees, while the standard library sin() and cos() functions work with radians.  I converted the angle in my own rotation equations from degrees into radians, in an attempt to keep my OpenGL code as clean as possible.  The resulting conversion ensured that my OpenGL-rotated object remains aligned with the object I rotated myself.

3D Rotation: Theory (Part II)

In the previous post, we found the equations for aligning an arbitrary vector with the z axis, in order to perform a rotation around that vector.  What we failed to determine, by the end of the discussion, was how to return the scene to its original coordinate space, so that only the object we rotated around the axis vector appeared to move.  We mentioned "undoing" the axis-alignment rotations, but didn't go into detail.

It turns out to be pretty simple.  Recall that we first made a clockwise rotation around the z axis, followed by a clockwise rotation around the y axis.  In order to return the scene to its original coordinate space, we need to first make a counter-clockwise rotation around the y axis, followed by a counter-clockwise rotation around the z axis.  Intuitively, the rotation angles are the same as those used for the axis-alignment rotations.  That is, to "undo" the rotation around the z axis, you must simply rotate in the opposite direction, through the original angle (only backwards).

It is possible to calculate new values of (x, y, z) for every point we want to rotate around the vector, using combinations of (and variations on) the equations from the previous post.  A given point's coordinates would have to be applied to each equation in turn, however, unless we could find some easy way to combine all of the equations, and apply that result to each of the points we want to rotate.

I mentioned before that the equations can be represented by matrices.  It turns out that matrices are ideal for these kinds of chain-transformations.  For our purposes, we could use 3x3 matrices for all of our rotational needs.  However, if we wished to represent any translation transformations in matrix form, a 3x3 matrix is not sufficient.   Consider the z component of a translation: z` = z + z_t.  In a 3x3 matrix representation, it is impossible to represent z except in terms of x and y.  With a 4x4 matrix, however, the translation is easy to find:

That bottom row deals with something called homogeneous coordinates, which basically means we're representing our three-dimensional world in a four-dimensional space, with a fixed fourth coordinate (much like how we moved our rotations into a two-dimensional problem within three-dimensional space).  For our purposes, we'll avoid tweaking that row as much as possible.

It is also easy to find the matrices for rotation around each of the standard axes, using the two-dimensional rotation equations we found previously:

We use the same equations for rotation around the y axis, substituting z for x and x for y:

The same technique applies to rotation around the x axis, substituting y for x and z for y:

Remember that, in order to perform a clockwise rotation (which is how we'll be moving our axis vector) the sign of each of the sin terms will need to be switched.

In the previous post, we found the angles of rotation (in terms of u, v and w) required to align the axis vector with the z axis.  With a minor variation, we can plug those values into the (inverted) rotation matrices:

Here's the variation:

Now that we've got our matrices defined, we need to understand how to use them.  If Rz is the matrix representing the rotation around the z axis, and P is a point we're rotating (represented as a 4x1 matrix), then RzP is the product of the two matrices (resulting in P`--our new point).  We can continue the chain, to rotate around the y axis (using the rotation matrix around y, Ry): RyP` = Ry(RzP).

One property of matrices is that they're associative in multiplication, so Ry(RzP) = (RyRz)P.

The matrix multiplication RyRz is the transformation to align our axis vector with the z axis.  We can take the result of that transformation, and add on the rotation about the axis vector, R: (RRyRz)P.

Once again, we have reached the point at which we need to "undo" our initial rotation transformations, in order to return the scene to its original coordinate space.  The last rotation we performed which we want to undo is the rotation around the y axis, Ry.  The transformation to undo that rotation, we'll call Ry^-1.  Appending that operation gives us (Ry^-1RRyRz)P.  Likewise, the transformation to undo the original rotation, we'll call Rz^-1, so (Rz^-1Ry^-1RRyRz)P.  So the full transformation we need to apply to each point we're rotating is Rz^-1Ry^-1RRyRz.

We're using a common matrix notation to denote an inverse transformation.  In the case of a rotation, an inverse is simply the rotation through the same angle, though in the opposite direction (so we switch the signs of each sine in our matrix).  It turns out that the matrix for the opposite rotation is the inverse matrix for the original rotation.  Mathematically, A^-1A = AA^-1 = I, where A is an invertible square matrix, and I is the identity matrix.  There are many matrix tutorials online, so I won't bother to explain these terms.

For our inverted rotation matrices, Rz^-1 and Ry^-1,  we can plug in the values for the rotation angles, using a counter-clockwise rotation (remember we used a clockwise rotation above).

Once we have all of our matrices figured out, we can multiply them all together (in sequence--order is important) to obtain a single transformation matrix, T.  We can multiply each point we wish to rotate (every vertex of a complex object, for example) by T to obtain their new positions in the original coordinate space.

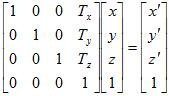
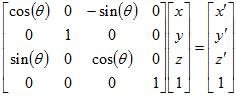
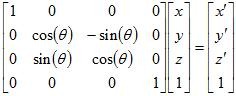
3D Rotation: Theory (Part I)

Rotating a set of points around an arbitrary axis in three dimensions takes a few steps, and can therefore be a little intimidating to grasp the concept. The main idea, though, is that the scene can be transformed so that the arbitrary axis becomes the z-axis.  At that point, the rotation can be considered a two-dimensional rotation (with the z-component of the rotating points remaining unchanged).  It then suffices to undo the original axis-alignment transformation, to put the arbitrary axis back in its original location.

If your arbitrary axis is part of an orthogonal set (in three dimensions, that is three axis at right angles to one another), I believe you can perform a simple change-of-basis transformation.  I haven't done the math on that, though, since it's a special case of what I'm attempting generally.

The two-dimensional rotation equations can be applied in any of the three basic planes (xy, xz, yz).  Given the x, y and z components of the axis vector (which we'll call u, v and w, respectively), we can determine the angles to use in the 2D rotations.  We'll first rotate the scene around the z axis so that the axis vector lies in the xz plane.  Next, we'll rotate the scene around the y axis so that the axis vector lies along the positive z axis.

The angle of rotation around the z axis (α) is found in terms of u and v (the lengths of the components orthogonal to the z axis):

We can apply the angle (α) to the two-dimensional rotation equation.  We must be careful to note, however, that the rotation in this case is clockwise (the previously-derived equations are for a counter-clockwise rotation).  We can simply use a negative angle, noting that cos(-θ) = cos(θ) and sin(-θ) = -sin(θ):

These equations, like those for the two-dimensional rotation, can be represented in matrix form.

The next step is to rotate the resulting vector around the y axis, until it lies along the z axis.  Looking from the positive y axis, the rotation onto the z axis is another clockwise rotation.  The components we'll use to find the angle of rotation (β), are a little more complicated this time.  Along the z axis is w (simple enough), but along the x axis, the value is the length of the original vector's projection into the xy plane ().

As before, we find the angle of rotation around the axis:

Once again, we apply this angle to the two-dimensional rotation equations, noting that we're using different axes.  What was originally x is now z, and y has become x.

Applying these equations, the axis of rotation will become the new z axis.  As was stated previously, the problem can be treated at this point like a two-dimensional rotation in the xy plane.  After that, these transformations to rotate the axis vector must be undone.  Matrix math can help significantly with that, and will be explored in the next post.