Translate
Derivation
Scale
Derivation
Rotate Around z-axis
Counter-ClockwiseDerivation
ClockwiseDerivation
Rotate Around y-axis
Counter-ClockwiseDerivation
ClockwiseDerivation
Rotate Around x-axis
Counter-ClockwiseDerivation
ClockwiseDerivation
Rotate Around Arbitrary Axis
—Defined by the unit vector (u, v, w)
Counter-Clockwise
Derivation
Clockwise
Derivation
Derivation: Translate
Derivation: Scale
Derivation: Rotate Around z-axis (Counter-Clockwise)
Derivation: Rotate Around z-axis (Clockwise)


Derivation: Rotate Around y-axis (Counter-Clockwise)


Derivation: Rotate Around y-axis (Clockwise)


Derivation: Rotate Around x-axis (Counter-Clockwise)


Derivation: Rotate Around x-axis (Clockwise)


Derivation: Rotate Around Arbitrary Axis (Counter-Clockwise)
- Rotate vector around z-axis (clockwise): Rz
- Rotate vector around y-axis (clockwise): Ry
- Rotate around vector (counter-clockwise): R
- Rotate vector around y-axis (counter-clockwise)*: Ry-1
- Rotate vector around z-axis (counter-clockwise)*: Rz-1
Total Rotation Transformation: Rz-1Ry-1RRyRz
= (Rz-1Ry-1)(R)(RyRz)
First and Last Rotations (Rz and Rz-1)


Second and Second-to-Last Rotations (Ry and Ry-1)


Middle rotation (R)

First two rotations combined (RyRz)

Final two rotations combined (Rz-1Ry-1)

Final three rotations combined (Rz-1Ry-1R)

Entire transformation ((Rz-1Ry-1R)(RyRz))




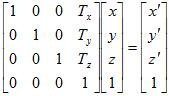




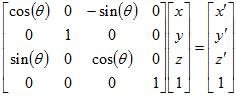
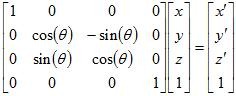





No comments:
Post a Comment