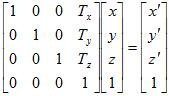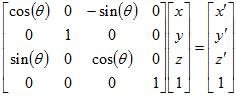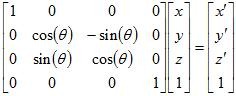OpenGL doesn’t have a camera, per se, like you might find in a traditional CAD application. 
Instead, it renders to the screen the view from the original origin, looking along the z-axis toward the negative direction (that is, z+ is coming out of the screen toward you). The x-axis is horizontal, with x+ going to the right side of the screen, and the y-axis is vertical, with y+ going to the top of the screen. The origin starts out centered in the widget that handles the rendering.
Using OpenGL is somewhat like trying to take a group photo in front of a landmark, where the camera stays in one position and the people are themselves moved around within the scene. In order to get the appearance of moving the camera, the entire OpenGL scene can be moved.
There are two basic ways of viewing an OpenGL world: perspective and orthographic views. There are various OpenGL tutorials which discuss the differences between the two, and how to set them up. It suffices me to mention that I’m using a perspective view, since it provides a more "real" 3D experience.
Three basic transformations can be performed in OpenGL: translate, rotate, and scale. Each transformation only affects the objects drawn after the transformation is made. Translate moves the origin to a new position; rotate changes the directions of the axes; scale changes the size of the basic unit.
Each object in the 3D world should be drawn in its own coordinate space—that is, with the origin (0, 0, 0) and the standard axes having meaning in the context of the object, without regards to any other object. In my game, the player agent's origin is quite different from the maze's origin, and is also quite different from the origin of any other agent. Each agent may have a different orientation from another, as far as the maze is concerned, but "forward" is always along the agent's own y-axis. It is possible that agents may experience life on different scales (an ant compared to a giant, for example), but for my purposes, scaling is largely ignored.
Transformations are the way to set the origin and axes properly so that, when the agent (or other object) is drawn, it is done within its own coordinate space. In the case of a third-person camera, a transformation should occur to place the agent's origin 
at some point in front of the camera. We will use a translate to move the origin ten units along the z-axis into the screen (in the negative direction): glTranslated(0, 0, –10). From this point forward, any operations performed will refer to the new origin. (The image to the right demonstrates the translate transformation.)
My world will assume that the xy-plane is horizontal, with z+ pointing toward the sky. If I were to draw the maze, at this point, the camera would be looking down on it from directly overhead. I would prefer to see the world from an over-the-shoulder kind of view, so I will need to perform a rotate transformation. My player is facing the y+ direction (along the green line, in the image above), so to move the camera so that it is facing the same general direction, I will have to rotate around the x-axis (the red line). A positive angle of rotation will point the y-axis more toward the camera, which is opposite the effect we're trying to create.
In the image to the right, the original axis orientation is shown using dashed lines, while solid lines show the orientation after the rotation around the x-axis has been performed. The cylinder demonstrates the position of the agent, relative to the camera. This gives us an over-the-head view (if we were going for a true over-the-shoulder view, we would have simply translated the origin along the x-axis before drawing the object).
Here is another perspective on the same scene, showing the agent's cylinder in its own coordinate space. Note that the axes look more traditional, with the xy-plane lying horizontally. Note also that we have also performed another translate transformation. In order to begin drawing the maze in its own coordinate space, the origin must be moved to the proper location.
I consider this to be the world coordinate space. Everything, from this point forward, can be built in terms of the current position, without worrying about the camera. Before performing any further transformations, use glPushMatrix() to store the current position, and the corresponding glPopMatrix() will return you to working in world coordinate space.
***
Note that this is not the exact series of transformations and drawing that I'm actually using. For my program, I'm expecting any number of agents, any one of which could be followed by the camera. While it's possible to do things exactly as I've done here, and simply draw the currently-followed agent separately from the other agents, it makes much more sense to me to draw all of the agents at the same time. In that case, the initial transformations are the same, to get the camera into the proper position. However, the agent is not drawn until after the world coordinate space is determined—along with all the other agents.
Note also that I did not give my cylindrical agent in this example any rotation within the world coordinate space. That rotation would have occurred immediately before the translation in the last image, after the agent had been drawn (so it would continue to face forward). If the agent were to look 45 degrees to the right, the scene would instead be rotated 45 degrees to the left (counter-clockwise, around the z-axis).
